Fairplay describes a protocol by which two parties can securely evaluate a function with the same guarantees as if they were using a trusted 3rd-party. This makes it possible to answer questions like the Millionaire's Problem without using a trusted 3rd-party. The Millionaire's Problem is: of two people, determine who has more money, without either of them learning exactly how much money the other person has.
This activity involves an extremely simplified version of the Millionaire's Problem. Alice and Bob are the millionaires, and they each have just 1-bit inputs. The expected behavior of the circuit is given in the truth table.
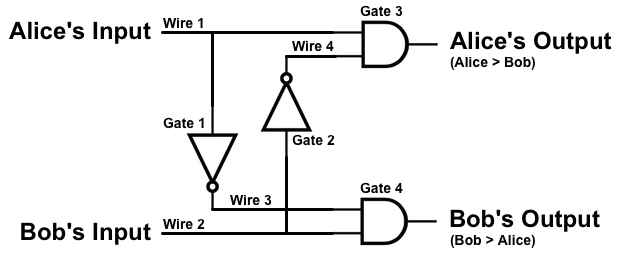
| Alice | Bob | Alice's Output | Bob's Output |
|---|---|---|---|
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
In this activity, you will play the part of Alice in the protocol. This means that Bob has given you an encrypted binary circuit and his and your inputs to that circuit. The encryption protocol has been simplified, and as a side-effect, you must use trial and error to decrypt the gates. You will know the gate has been successfully decrypted when an English word is revealed (or a binary digit, in the case of Alice's outputs).
You will only be able to (successfully) decrypt one output from each gate. To compute an output, enter the gate's number and the x and y keys into the hasher. Then, use this hashed value output to decrypt one of the outputs from the truth table.
For example, consider a gate number 42, which only has a single input. Given the input key "fridge", you should get the value "f68607aa93bbe88e769b5e6d136337fe48485fab" from the hasher. This gate has two encrypted outputs, "000c000c0040000700580051" and "000e0059004c0052005f0050". Try decrypting these with the result from the hasher. You should only be able to decrypt one of them.
Alice's Input: pepper
Bob's Input: toyota
Evaluate the encrypted circuit to find:
| x, Wire 1 | z, Wire 3 |
|---|---|
| XXXXXX | 000d005900440016004f0019 |
| XXXXXX | 0016005c005400040010001f |
| x, Wire 2 | z, Wire 4 |
|---|---|
| XXXXXX | 005800470016000e0003001e |
| XXXXXX | 000500570057000500590053 |
| x, Wire 1 | y, Wire 4 | z, Alice Output |
|---|---|---|
| XXXXXX | XXXXXX | 0006001b004a004d001d001d |
| XXXXXX | XXXXXX | 0005004d001e001b001e001c |
| XXXXXX | XXXXXX | 0007004d0017001f00180018 |
| XXXXXX | XXXXXX | 005200480016001800480017 |
| x, Wire 3 | y, Wire 2 | z, Bob Output |
|---|---|---|
| XXXXXX | XXXXXX | 005000580017005900560008 |
| XXXXXX | XXXXXX | 0045000b005200080059001f |
| XXXXXX | XXXXXX | 000700510047005e00030008 |
| XXXXXX | XXXXXX | 00000056004300580053005e |
Concatenates the inputs, then computes the SHA1 hash.
Gate Number:Attempts decryption by taking the exclusive-or of the supplied hash and hex-encoded ciphertext.
xor
Encrypts by taking the exclusive-or of the supplied hash and plaintext.
Not used for the activity, but included for completeness.